Fibonacci sequence

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted F_n. The sequence commonly starts from 0 and 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

F₂₀ = 6765
F₅₀ = 12586269025
F₁₀₀ = 354224848179261915075
F₅₀₀ = 139423224561697880139724382870407283950070256587697307264108962948325571622863290691557658876222521294125

Naive Approach

Compute the n-th Fibonacci number.

Input: An integer n.
Output: n-th Fibonacci number.

Input format - An integer n.
Output format - F_n
Constraints - 0 ≤ n ≤ 45.

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)


if __name__ == '__main__':
    _ = int(input())
    print(fibonacci(_))

The above algo works well for very small n. If we have n=100 it would take 56000 years to execute it at 1 GHz. Why it takes so much time because in recursion 1 value is calculated multiple times and hence it recomputes again and again.

Efficient Approach

So instead of stack we put loops and compute fibonacci numbers from scratch everytime.

create an array F [0 . . . n] 
F [0] ← 0
F [1] ← 1
for i from 2 to n:
	F [i] ← F [i − 1] + F [i − 2]
return F [n]

def fibonacci(n):
    fib=[]
    fib.append(0)
    fib.append(1)
    for i in range(2, n):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n-1]


if __name__ == '__main__':
    _ = int(input())
    print(fibonacci(_))

The right algorithm makes all the difference.

Greatest Common Divisor

The greatest common divisor GCD(a,b) of two positive integers a and b is the largest integer d that divides both a and b. The solution of the Greatest Common Divisor Problem was first described (but not discovered!) by the Greek mathematician Euclid twenty three centuries ago.

Naive Approach

Compute the greatest common divisor of two positive integers.

Input: Two positive integers a and b.
Output: The greatest common divisor of a and b.

Input format - Integers a and b (separated by a space).
Output format - GCD(a,b)
Constraints - 1 ≤ a,b ≤ 2 · 10⁹

def GCD(a, b):
    best = 0
    for i in range(1, a+b):
        if a % i == 0 and b % i == 0:
            best = i
    return best


if __name__ == '__main__':
    input_numbers = list(map(int, input().split()))
    print(GCD(input_numbers[0], input_numbers[1]))

This approach runs approximately for a+b and its very slow for a 20 digit number.

Efficient Approach

Let a′ be the remainder when a is divided by b, then

gcd(a, b) = gcd(a′, b) = gcd(b, a′)

So algorithm becomes :

if b = 0: 
	return a
a′ ← the remainder when a is
	divided by b 
return EuclidGCD(b, a′)

gcd(3918848, 1653264) 
= gcd(1653264, 612320) 
= gcd(612320, 428624)
= gcd(428624, 183696)
= gcd(183696, 61232)
= gcd(61232, 0)
=61232

def GCD(a, b):
    if b==0:
        return a
    c=a%b
    return GCD(b,c)


if __name__ == '__main__':
    input_numbers = list(map(int, input().split()))
    print(GCD(input_numbers[0], input_numbers[1]))

Asymptotic Notation

Computing runtimes is hard, as it depends on fine details of program and details of computer. So we measure runtime in a way that ignores constant multiples.

\[logn < \sqrt{n} < n < nlogn < n^2 < 2^n\]

Big O Notation

\(f(n) = O(g(n)) \text{(f is Big-O of g) or f<=g}\)
\(\text{if there exists constants N and c so that for all n>=N, f(n) <= c.g(n)}\)

3n² + 5n + 2 has the same growth rate as n²

This has several advantages :

Clarifies Growth rate
Cleans up notation
Can ignore complicated details

Common Rules :

Multiplicative constants can be omitted
n^a < n^b for 0 < a < b
n^a < n^b (a > 0, b > 1)
(logn)^a < n^b (a, b > 0)
Smaller terms can be omitted

Calculating Big(O) :

Operation	Runtime
create an array F[0…n]	O(n)
F[0] = 0	O(1)
F[1] = 1	O(1)
for i from 2 to n:	Loop O(n) times
F[i] = F[i-1] + F[i-2]	O(n) as F[i] is very large number
return F[n]	O(1)

Total = O(n) + O(1) + O(1) + O(n).O(n) + O(1) = O(n²)

Plotting Graphs

Import modules :

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

Plotting = 7n² + 6n + 5 for 1<=n<=100

n = np.linspace(1, 100)
plt.plot(n, 7 * n * n + 6 * n + 5)
plt.show()

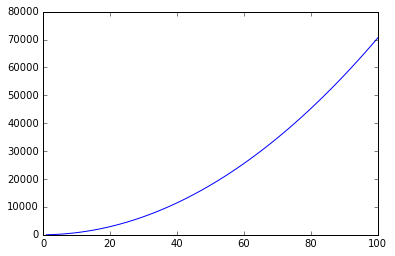
Plot_1

Smaller terms can be omitted :

n = np.linspace(1, 100)
plt.plot(n, 7 * n * n + 6 * n + 5, label="7n^2+6n+5")
plt.plot(n, 7 * n * n, label="7n^2")
plt.legend(loc='upper left')
plt.show()

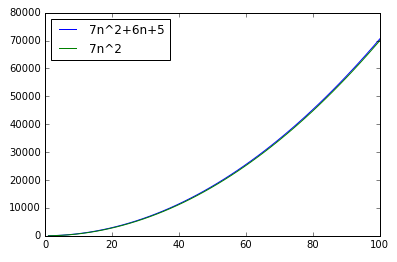
Plot_2

Out of two polynomials, the one with larger degree grows faster :

n = np.linspace(1, 10)
plt.plot(n, n, label="n")
plt.plot(n, n * n, label="n^2")
plt.plot(n, n * n * n, label="n^3")
plt.legend(loc='upper left')
plt.show()

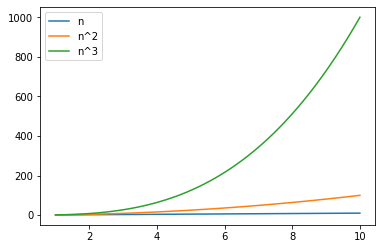
Plot_3

Levels of Design

Naive Algorithm: Definition to algorithm. Slow.
Algorithm by way of standard Tools: Standard techniques.
Optimized Algorithm: Improve existing algorithm.
Magic Algorithm: Unique insight.

Programming Challenge #2

1. Fibonacci Numbers

Compute the n-th Fibonacci number.

Input: An integer n.
Output: n-th Fibonacci number.

Input format - An integer n.
Output format - F_n
Constraints - 0 ≤ n ≤ 45.

Example 1

Solution

def fibonacci(n):
    fib=[]
    fib.append(0)
    fib.append(1)
    for i in range(2, n):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n-1]


if __name__ == '__main__':
    _ = int(input())
    print(fibonacci(_))

2. Last Digit of Fibonacci Numbers

Compute the last digit of the n-th Fibonacci number.

Input: An integer n.
Output: The last digit of the n-th Fibonacci number.

Input format - An integer n.
Output format - F_n
Constraints - 0 ≤ n ≤ 10⁶.

Example 1

Solution

def fibonacci(n):
    fib=[]
    fib.append(0)
    fib.append(1)
    for i in range(2, n+1):
        fib.append((fib[i-1] + fib[i-2])%10)
    return fib[n]


if __name__ == '__main__':
    _ = int(input())
    if _ == 0:
        print(0)
    elif _ == 1:
        print(1)
    else:
        print(fibonacci(_))

3. Greatest Common Divisor

Compute the greatest common divisor of two positive integers.

Input: Two positive integers a and b.
Output: The greatest common divisor of a and b.

Input format - Integers a and b (separated by a space).
Output format - GCD(a,b)
Constraints - 1 ≤ a,b ≤ 2 · 10⁹

Example 1

28851538 1183019

Solution

def GCD(a, b):
    if b==0:
        return a
    c=a%b
    return GCD(b,c)


if __name__ == '__main__':
    input_numbers = list(map(int, input().split()))
    print(GCD(input_numbers[0], input_numbers[1]))

4. Least Common Multiple

Compute the least common multiple of two positive integers.

Input: Two positive integers a and b.
Output: The least common multiple of a and b.

Input format - Integers a and b (separated by a space).
Output format - LCM(a,b)
Constraints - 1 ≤ a,b ≤ 2 · 10⁷

Example 1

761457 614573

467970912861

Solution

def GCD(a, b):
    if b==0:
        return a
    c=a%b
    return GCD(b,c)


if __name__ == '__main__':
    input_numbers = list(map(int, input().split()))
    print((int)((input_numbers[0]*input_numbers[1])/GCD(input_numbers[0], input_numbers[1])))

5. Huge fibonacci number

Compute the n-th Fibonacci number modulo m.

Input: Two positive integers n and m.
Output: n-th Fibonacci number modulo m.

Input format - Integers n and m (separated by a space).
Output format - F_n mod m.
Constraints - 1 ≤ n ≤ 2 · 10¹⁴, 2 ≤ m ≤ 10³

Example 1

2816213588 239

Solution

This problem can be solved using the properties of Pisano Period. For a given value of N and M >= 2, the series generated with F_i modulo M (for i in range(N)) is periodic.

The period always starts with 01. The Pisano Period is defined as the length of the period of this series. So to compute, say F₂₀₁₉ mod 5, we’ll find the remainder of 2019 when divided by 20 (Pisano Period of 5 is 20). 2019 mod 20 is 19. Therefore, F₂₀₁₉ mod 5 = F₁₉ mod 5 = 1. This property is true in general.

# python3
n, m = [int(i) for i in input().split()]

if n<=1:
    print(n)  
    quit()

pisano = {2: 3, 3: 8, 4: 6, 5: 20, 6: 24, 7: 16, 8: 12, 9: 24, 10: 60, 11: 10, 12: 24, 13: 28, 14: 48, 15: 40, 16: 24, 17: 36, 18: 24, 19: 18, 20: 60, 21: 16, 22: 30, 23: 48, 24: 24, 25: 100, 26: 84, 27: 72, 28: 48, 29: 14, 30: 120, 31: 30, 32: 48, 33: 40, 34: 36, 35: 80, 36: 24, 37: 76, 38: 18, 39: 56, 40: 60, 41: 40, 42: 48, 43: 88, 44: 30, 45: 120, 46: 48, 47: 32, 48: 24, 49: 112, 50: 300, 51: 72, 52: 84, 53: 108, 54: 72, 55: 20, 56: 48, 57: 72, 58: 42, 59: 58, 60: 120, 61: 60, 62: 30, 63: 48, 64: 96, 65: 140, 66: 120, 67: 136, 68: 36, 69: 48, 70: 240, 71: 70, 72: 24, 73: 148, 74: 228, 75: 200, 76: 18, 77: 80, 78: 168, 79: 78, 80: 120, 81: 216, 82: 120, 83: 168, 84: 48, 85: 180, 86: 264, 87: 56, 88: 60, 89: 44, 90: 120, 91: 112, 92: 48, 93: 120, 94: 96, 95: 180, 96: 48, 97: 196, 98: 336, 99: 120, 100: 300, 101: 50, 102: 72, 103: 208, 104: 84, 105: 80, 106: 108, 107: 72, 108: 72, 109: 108, 110: 60, 111: 152, 112:
48, 113: 76, 114: 72, 115: 240, 116: 42, 117: 168, 118: 174, 119: 144, 120: 120, 121: 110, 122: 60, 123: 40, 124: 30, 125: 500, 126: 48, 127: 256, 128: 192, 129: 88, 130: 420, 131: 130, 132: 120, 133: 144, 134: 408, 135: 360, 136: 36, 137: 276, 138: 48, 139: 46, 140: 240, 141: 32, 142: 210, 143: 140, 144: 24, 145: 140, 146: 444, 147: 112, 148: 228, 149: 148, 150: 600, 151: 50, 152: 36, 153: 72, 154: 240, 155: 60, 156: 168, 157: 316, 158: 78, 159: 216, 160: 240, 161: 48, 162: 216, 163: 328, 164: 120, 165: 40, 166: 168, 167: 336, 168: 48, 169: 364, 170: 180, 171: 72, 172: 264, 173: 348, 174: 168, 175: 400, 176: 120, 177: 232, 178: 132, 179: 178, 180: 120, 181: 90, 182: 336, 183: 120, 184: 48, 185: 380, 186: 120, 187: 180, 188: 96, 189: 144, 190: 180, 191: 190, 192: 96, 193: 388, 194: 588, 195: 280, 196: 336, 197: 396, 198: 120, 199: 22, 200: 300, 201: 136, 202: 150, 203: 112, 204: 72, 205: 40, 206: 624, 207:
48, 208: 168, 209: 90, 210: 240, 211: 42, 212: 108, 213: 280, 214: 72, 215: 440, 216: 72, 217: 240, 218: 108, 219: 296, 220: 60, 221: 252, 222: 456, 223: 448, 224: 48, 225: 600, 226: 228, 227: 456, 228: 72, 229: 114, 230: 240, 231: 80, 232: 84, 233: 52, 234: 168, 235: 160, 236: 174, 237: 312, 238: 144, 239: 238, 240: 120, 241: 240, 242: 330, 243: 648, 244: 60, 245:
560, 246: 120, 247: 252, 248: 60, 249: 168, 250: 1500, 251: 250, 252: 48, 253: 240, 254: 768, 255: 360, 256: 384, 257: 516, 258: 264, 259: 304, 260: 420, 261: 168, 262: 390, 263: 176,
264: 120, 265: 540, 266: 144, 267: 88, 268: 408, 269: 268, 270: 360, 271: 270, 272: 72, 273: 112, 274: 276, 275: 100, 276: 48, 277: 556, 278: 138, 279: 120, 280: 240, 281: 56, 282: 96, 283: 568, 284: 210, 285: 360, 286: 420, 287: 80, 288: 48, 289: 612, 290: 420, 291: 392, 292: 444, 293: 588, 294: 336, 295: 580, 296: 228, 297: 360, 298: 444, 299: 336, 300: 600, 301:
176, 302: 150, 303: 200, 304: 72, 305: 60, 306: 72, 307: 88, 308: 240, 309: 208, 310: 60, 311: 310, 312: 168, 313: 628, 314: 948, 315: 240, 316: 78, 317: 636, 318: 216, 319: 70, 320: 480, 321: 72, 322: 48, 323: 36, 324: 216, 325: 700, 326: 984, 327: 216, 328: 120, 329: 32, 330: 120, 331: 110, 332: 168, 333: 456, 334: 336, 335: 680, 336: 48, 337: 676, 338: 1092, 339: 152, 340: 180, 341: 30, 342: 72, 343: 784, 344: 264, 345: 240, 346: 348, 347: 232, 348: 168, 349: 174, 350: 1200, 351: 504, 352: 240, 353: 236, 354: 696, 355: 140, 356: 132, 357: 144, 358: 534, 359: 358, 360: 120, 361: 342, 362: 90, 363: 440, 364: 336, 365: 740, 366: 120, 367: 736, 368: 48, 369: 120, 370: 1140, 371: 432, 372: 120, 373: 748, 374: 180, 375: 1000, 376: 96, 377: 28, 378: 144, 379: 378, 380: 180, 381: 256, 382: 570, 383: 768, 384: 192, 385: 80, 386: 1164, 387: 264, 388: 588, 389: 388, 390: 840, 391: 144, 392: 336, 393: 520, 394: 396, 395: 780, 396: 120, 397: 796, 398: 66, 399: 144, 400: 600, 401: 200, 402: 408, 403: 420, 404: 150, 405: 1080, 406: 336, 407: 380, 408: 72, 409: 408, 410: 120, 411: 552, 412: 624, 413: 464, 414: 48, 415: 840, 416: 336, 417: 184, 418: 90, 419: 418, 420: 240, 421: 84, 422: 42, 423: 96, 424: 108, 425: 900, 426: 840, 427: 240, 428: 72, 429: 280, 430: 1320, 431: 430, 432: 72, 433: 868, 434: 240, 435: 280, 436: 108, 437: 144, 438: 888, 439: 438, 440: 60, 441: 336, 442: 252, 443: 888, 444: 456, 445: 220, 446: 1344, 447: 296, 448: 96, 449: 448, 450: 600, 451: 40, 452: 228, 453: 200, 454: 456, 455: 560, 456: 72, 457: 916, 458: 114, 459: 72, 460: 240, 461: 46, 462: 240, 463: 928, 464: 168, 465: 120, 466: 156, 467: 936, 468: 168, 469: 272, 470: 480, 471: 632, 472: 348, 473: 440, 474: 312, 475: 900, 476: 144, 477: 216, 478: 714, 479: 478, 480: 240, 481: 532, 482: 240, 483: 48, 484: 330, 485: 980, 486: 648, 487: 976, 488: 60, 489: 328, 490: 1680, 491: 490, 492: 120, 493: 252, 494: 252, 495: 120, 496: 120, 497: 560, 498: 168, 499: 498, 500: 1500, 501: 336, 502: 750, 503: 1008, 504: 48, 505: 100, 506:
240, 507: 728, 508: 768, 509: 254, 510: 360, 511: 592, 512: 768, 513: 72, 514: 516, 515: 1040, 516: 264, 517: 160, 518: 912, 519: 696, 520: 420, 521: 26, 522: 168, 523: 1048, 524: 390, 525: 400, 526: 528, 527: 180, 528: 120, 529: 1104, 530: 540, 531: 696, 532: 144, 533: 280, 534: 264, 535: 360, 536: 408, 537: 712, 538: 804, 539: 560, 540: 360, 541: 90, 542: 270, 543: 360, 544: 144, 545: 540, 546: 336, 547: 1096, 548: 276, 549: 120, 550: 300, 551: 126, 552: 48, 553: 624, 554: 1668, 555: 760, 556: 138, 557: 124, 558: 120, 559: 616, 560: 240, 561: 360, 562: 168, 563: 376, 564: 96, 565: 380, 566: 1704, 567: 432, 568: 420, 569: 568, 570: 360, 571: 570, 572: 420, 573: 760, 574: 240, 575: 1200, 576: 96, 577: 1156, 578: 612, 579: 776, 580: 420, 581: 336, 582: 1176, 583: 540, 584: 444, 585: 840, 586: 588, 587: 1176, 588: 336, 589: 90, 590: 1740, 591: 792, 592: 456, 593: 1188, 594: 360, 595: 720, 596: 444, 597: 88, 598: 336, 599: 598, 600: 600, 601: 600, 602: 528, 603: 408, 604: 150, 605: 220, 606: 600, 607: 1216, 608: 144, 609: 112, 610: 60, 611: 224, 612: 72, 613: 1228, 614: 264, 615: 40, 616: 240, 617: 1236, 618: 624, 619: 206, 620: 60, 621: 144, 622: 930, 623: 176, 624: 168, 625: None, 626: 1884, 627: 360, 628: 948, 629: 684, 630: 240, 631: 630, 632: 156, 633: 168, 634: 636, 635: 1280, 636: 216, 637: 112, 638: 210, 639: 840, 640: 960, 641: 640, 642: 72, 643: 1288, 644: 48, 645: 440, 646: 36, 647: 1296, 648: 216, 649: 290, 650: None, 651: 240, 652: 984, 653: 1308, 654: 216, 655: 260, 656: 120, 657: 888, 658: 96, 659: 658, 660: 120, 661: 220, 662: 330, 663: 504, 664: 168, 665: 720, 666: 456, 667: 336, 668: 336, 669: 448, 670: None, 671: 60, 672: 48, 673: 1348, 674: None, 675: 1800, 676: 1092, 677: 452, 678: 456, 679: 784, 680: 180, 681: 456, 682: 30, 683: 1368, 684: 72, 685: 1380, 686: None, 687: 456, 688: 264, 689:
756, 690: 240, 691: 138, 692: 348, 693: 240, 694: 696, 695: 460, 696: 168, 697: 360, 698: 174, 699: 104, 700: 1200, 701: 700, 702: 504, 703: 684, 704: 480, 705: 160, 706: 708, 707: 400, 708: 696, 709: 118, 710: 420, 711: 312, 712: 132, 713: 240, 714: 144, 715: 140, 716: 534, 717: 952, 718: 1074, 719: 718, 720: 120, 721: 208, 722: 342, 723: 240, 724: 90, 725: 700, 726: 1320, 727: 1456, 728: 336, 729: 1944, 730: None, 731: 792, 732: 120, 733: 1468, 734: None, 735: 560, 736: 48, 737: 680, 738: 120, 739: 738, 740: 1140, 741: 504, 742: 432, 743: 496,
744: 120, 745: 740, 746: None, 747: 168, 748: 180, 749: 144, 750: None, 751: 750, 752: 96, 753: 1000, 754: 84, 755: 100, 756: 144, 757: 1516, 758: 378, 759: 240, 760: 180, 761: 380, 762: 768, 763: 432, 764: 570, 765: 360, 766: 768, 767: 812, 768: 384, 769: 192, 770: 240, 771: 1032, 772: 1164, 773: 1548, 774: 264, 775: 300, 776: 588, 777: 304, 778: 1164, 779: 360, 780: 840, 781: 70, 782: 144, 783: 504, 784: 336, 785: 1580, 786: 1560, 787: 1576, 788: 396, 789: 176, 790: 780, 791: 304, 792: 120, 793: 420, 794: None, 795: 1080, 796: 66, 797: 228, 798: 144, 799: 288, 800: 1200, 801: 264, 802: 600, 803: 740, 804: 408, 805: 240, 806: 420, 807: 536, 808: 300, 809: 202, 810: 1080, 811: 270, 812: 336, 813: 1080, 814: 1140, 815: 1640, 816: 72, 817: 792, 818: 408, 819: 336, 820: 120, 821: 820, 822: 552, 823: 1648, 824: 624, 825: 200, 826: 1392, 827: 1656, 828: 48, 829: 276, 830: 840, 831: 1112, 832: 672, 833: 1008, 834: 552, 835: 1680, 836: 90, 837: 360, 838: 1254, 839: 838, 840: 240, 841: 406, 842: 84, 843: 56, 844: 42, 845: 1820, 846: 96, 847: 880, 848: 216, 849: 568, 850: 900, 851: 912, 852: 840, 853: 1708, 854: 240, 855: 360, 856: 72, 857: 1716, 858: 840, 859: 78, 860: 1320, 861: 80, 862: 1290, 863: 1728, 864: 144, 865: 1740, 866: None, 867: 1224, 868: 240, 869: 390, 870: 840, 871: 952, 872: 108, 873: 1176, 874: 144, 875: None, 876: 888, 877: 1756, 878: 438, 879: 1176, 880: 120, 881: 176, 882: 336, 883: 1768, 884: 252, 885: 1160, 886: 888, 887: 1776, 888:
456, 889: 256, 890: 660, 891: 1080, 892: 1344, 893: 288, 894: 888, 895: 1780, 896: 192, 897: 336, 898: 1344, 899: 210, 900: 600, 901: 108, 902: 120, 903: 176, 904: 228, 905: 180, 906:
600, 907: 1816, 908: 456, 909: 600, 910: 1680, 911: 70, 912: 72, 913: 840, 914: None, 915: 120, 916: 114, 917: 1040, 918: 72, 919: 102, 920: 240, 921: 88, 922: 138, 923: 140, 924: 240, 925: 1900, 926: None, 927: 624, 928: 336, 929: 928, 930: 120, 931: 1008, 932: 156, 933: 1240, 934: 936, 935: 180, 936: 168, 937: 1876, 938: 816, 939: 1256, 940: 480, 941: 470, 942: 1896, 943: 240, 944: 696, 945: 720, 946: 1320, 947: 1896, 948: 312, 949: 1036, 950: 900, 951: 1272, 952: 144, 953: 212, 954: 216, 955: 380, 956: 714, 957: 280, 958: 1434, 959: 1104, 960: 480, 961: 930, 962: 1596, 963: 72, 964: 240, 965: 1940, 966: 48, 967: 176, 968: 660, 969: 72, 970: None, 971: 970, 972: 648, 973: 368, 974: None, 975: 1400, 976: 120, 977: 652, 978: 984, 979: 220, 980: 1680, 981: 216, 982: 1470, 983: 1968, 984: 120, 985: 1980, 986: 252, 987: 32, 988: 252, 989: 528, 990: 120, 991: 198, 992: 240, 993: 440, 994: 1680, 995: 220, 996: 168, 997: 1996, 998: 498, 999: 1368, 1000: 1500}

lesser = n%pisano[m]
if lesser<=1:
    print(lesser)
    quit()

def fibo(n, m):
    lesser = n%pisano[m]
    a, b = 0, 1
    for _ in range(2,lesser+1):
        c = a + b
        b, a = c, b
    print(c%m)

fibo(lesser, m)

6. Last Digit of the Sum of Fibonacci Numbers

Compute the last digit of F₀ + F₁ + · · · + F_n.

Input: An integer n.
Output: The last digit of F₀ + F₁ + · · · + F_n.

Input format - An integer n.
Output format - (F₀ + F₁ + · · · + F_n)mod10.
Constraints - 0 ≤ n ≤ 10¹⁴

Example 1

Solution

The idea is to notice that the last digits of fibonacci numbers also occur in sequences of length 60 (from the previous problem: since pisano peiod of 10 is 60). Irrespective of how large n is, its last digit is going to have appeared somewhere within the sequence. Two Things apart from edge case of 10 as last digit.

Sum of nth Fibonacci series = F(n+2) -1

Then pisano period of module 10 = let n+2 mod (60) = m then find F(m) mod(10)-1

n = int(input())

if n<=1:
    print(n)  
    quit()


lesser = (n+2)%60
if lesser==1:
    print(0)
    quit()
elif lesser==0:
    print(9)
    quit()
def fibo(n):
    a,b = 0, 1
    for _ in range(2,lesser+1):
        c = a+b
        c = c%10
        b, a = c, b
    if c!=0:
        print(c-1)
    else:
        print(9)
fibo(lesser)

7. Last Digit of the Sum of Fibonacci Numbers Again

Given two non-negative integers 𝑚 and 𝑛, where 𝑚 ≤ 𝑛, find the last digit of the sum F_m + F_m+1 + · · · + F_n.

Input: The input consists of two non-negative integers 𝑚 and 𝑛 separated by a space.
Output: The last digit of F_m + F_m+1 + · · · + F_n.

Example 1

10 200

Solution

Call the previous function twice, once for n and again for m. Subtract both values.

m, n = [int(i) for i in input().split()]

if n<=1:
    print(n)  
    quit()

lesser_n = (n+2)%60
lesser_m = (m+1)%60

def fibo(n):
    a,b = 0, 1
    for i in range(2,n+1):
        c = a+b
        c = c%10
        b, a = c, b
    return (c-1)
if lesser_n<=1:
    a = lesser_n-1
else:
    a = fibo(lesser_n)
if lesser_m<=1:
    b = lesser_m-1
else:
    b = fibo(lesser_m)
if a>=b:
    print(a-b)
else:
    print(10+a-b)

8. Last Digit of the Sum of Squares of Fibonacci Numbers

Compute the last digit of F₀² + F₁² + · · · + F_n².

Input: The input n.
Output: The last digit of F₀² + F₁² + · · · + F_n².

Example 1

1234567890

Solution

There is a theoram :

\[F_1^2 + F_1^2+...+F_1^2 = F_nF_{n+1}\]

n = int(input())
lesser_n = n%60
lesser_nplus = (n+1)%60

def fibo(n):
    a, b = 0, 1
    for _ in range(2, n+1):
        c = a+b
        c = c% 10
        b, a = c, b
    return c

if lesser_n<=1:
    a = lesser_n
else:
    a = fibo(lesser_n)
if lesser_nplus<=1:
    b = lesser_nplus
else:
    b = fibo(lesser_nplus)

 
print((a*b)%10)

Rohan Verma

Learning Machine Learning and other programming stuff

Fibonacci sequence

Naive Approach

Efficient Approach

Greatest Common Divisor

Naive Approach

Efficient Approach

Asymptotic Notation

Big O Notation

Plotting Graphs

Levels of Design

Programming Challenge #2

1. Fibonacci Numbers

Example 1

Solution

2. Last Digit of Fibonacci Numbers

Example 1

Solution

3. Greatest Common Divisor

Example 1

Solution

4. Least Common Multiple

Example 1

Solution

5. Huge fibonacci number

Example 1

Solution

6. Last Digit of the Sum of Fibonacci Numbers

Example 1

Solution

7. Last Digit of the Sum of Fibonacci Numbers Again

Example 1

Solution

8. Last Digit of the Sum of Squares of Fibonacci Numbers

Example 1

Solution