1. Stable Arrangement of Rooks
You have an n×n chessboard and k rooks. Rows of this chessboard are numbered by integers from 1 to n from top to bottom and columns of this chessboard are numbered by integers from 1 to n from left to right. The cell (x,y) is the cell on the intersection of row x and collumn y for 1≤x≤n and 1≤y≤n.
The arrangement of rooks on this board is called good, if no rook is beaten by another rook.
A rook beats all the rooks that shares the same row or collumn with it.
The good arrangement of rooks on this board is called not stable, if it is possible to move one rook to the adjacent cell so arrangement becomes not good. Otherwise, the good arrangement is stable. Here, adjacent cells are the cells that share a side.
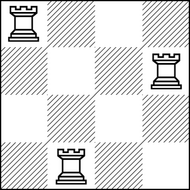
Such arrangement of 3 rooks on the 4×4 chessboard is good, but it is not stable: the rook from (1,1) can be moved to the adjacent cell (2,1) and rooks on cells (2,1) and (2,4) will beat each other. Please, find any stable arrangement of k rooks on the n×n chessboard or report that there is no such arrangement.
Input
The first line contains a single integer t (1≤t≤100) — the number of test cases.
The first line of each test case contains two integers n, k (1≤k≤n≤40) — the size of the chessboard and the number of rooks.
Output
If there is a stable arrangement of k rooks on the n×n chessboard, output n lines of symbols . and R. The j-th symbol of the i-th line should be equals R if and only if there is a rook on the cell (i,j) in your arrangement.
If there are multiple solutions, you may output any of them.
If there is no stable arrangement, output −1.
Example
5
3 2
3 3
1 1
5 2
40 33
..R
...
R..
-1
R
.....
R....
.....
....R
.....
-1
Note
In the first test case, you should find stable arrangement of 2 rooks on the 3×3 chessboard. Placing them in cells (3,1) and (1,3) gives stable arrangement.
In the second test case it can be shown that it is impossbile to place 3 rooks on the 3×3 chessboard to get stable arrangement.
Solution
The problem is easier then it looks like. So basically what the setter is trying to say is that we have to place ‘k’ rooks on an nxn chessboard in such a way that :
- No rook is beaten by another rook
- Even if we move any rook to its adjacent sides then also it shouldn’t beat any other rook on the chessboard.
So if in above image, we move Rook R1 (at 1,1) to it’s adjacent side (2,1 or 1,2) than also it shouldn’t beat any other rook. This condition should be satisfied by every rook on the chessboard. To understand it more clearly let’s look at below figure.
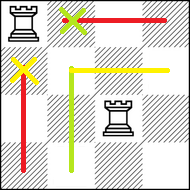
Initially the rook is at (1,1) position. So no rook should be in any row/column crossed of by red colour. If we move rook to its adjacent side (denoted by green and yellow ‘X’ mark) then no rook should be in row/column denoted by yellow and green colour respectively. So effectively 1 rook is occupying 2 rows/columns.
Since it is an nxn chessboard and to make k rooks stable each rook requires 2 rows/columns so we can come up with a simple solution that if k > [(n+1)/2] then there is no stable arrangement. Moreover, we can always place k≤⌊(n+1)/2⌋ rooks into cells [(1,1), (3,3), …, (2k−1,2k−1)]. Such arrangement is stable because after moving any rook to the neighbouring row it will be in the same collumn and in the even numbered row where there are no other rooks. The same applies for moving rook to the neighbouring collumn.
Since we have set a baseline lets try to code it :
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main() {
int t,n,k,rooks_placed=0;
cin>>t;
while(t--)
{
cin>>n>>k;
if(k>(n+1)/2)
{
cout<<"-1"<<endl;
}
else
{
rooks_placed=0;
for(int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
{
if(i==j && i%2==0 && rooks_placed<k)
{
rooks_placed++;
cout<<"R";
}
else
cout<<".";
}
cout<<endl;
}
}
}
return 0;
}
The above solution passes as expected. The variable “rooks_placed” is a counter to keep track of how many rooks we have already placed on the chessboard. It should not be more than ‘k’.
2. Integers Shop
The integers shop sells n segments. The i-th of them contains all integers from li to ri and costs ci coins.
Tomorrow Vasya will go to this shop and will buy some segments there. He will get all integers that appear in at least one of bought segments. The total cost of the purchase is the sum of costs of all segments in it.
After shopping, Vasya will get some more integers as a gift. He will get integer x as a gift if and only if all of the following conditions are satisfied:
Vasya hasn’t bought x. Vasya has bought integer l that is less than x. Vasya has bought integer r that is greater than x. Vasya can get integer x as a gift only once so he won’t have the same integers after receiving a gift.
For example, if Vasya buys segment [2,4] for 20 coins and segment [7,8] for 22 coins, he spends 42 coins and receives integers 2,3,4,7,8 from these segments. He also gets integers 5 and 6 as a gift.
Due to the technical issues only the first s segments (that is, segments [l1,r1],[l2,r2],…,[ls,rs]) will be available tomorrow in the shop.
Vasya wants to get (to buy or to get as a gift) as many integers as possible. If he can do this in differents ways, he selects the cheapest of them.
For each s from 1 to n, find how many coins will Vasya spend if only the first s segments will be available.
Input
The first line contains a single integer t (1≤t≤1000) — the number of test cases.
The first line of each test case contains the single integer n (1≤n≤105) — the number of segments in the shop.
Each of next n lines contains three integers li, ri, ci (1≤li≤ri≤109,1≤ci≤109) — the ends of the i-th segments and its cost.
It is guaranteed that the total sum of n over all test cases doesn’t exceed 2⋅105.
Output
For each test case output n integers: the s-th (1≤s≤n) of them should be the number of coins Vasia will spend in the shop if only the first s segments will be available.
Example
3
2
2 4 20
7 8 22
2
5 11 42
5 11 42
6
1 4 4
5 8 9
7 8 7
2 10 252
1 11 271
1 10 1
20
42
42
42
4
13
11
256
271
271
Note
In the first test case if s=1 then Vasya can buy only the segment [2,4] for 20 coins and get 3 integers.
The way to get 7 integers for 42 coins in case s=2 is described in the statement.
In the second test case note, that there can be the same segments in the shop.
Solution
Let L be the minimum integer Vasya will buy and R be the maximum integer Vasya will buy. Then it is easy to see that he will get all integers between L and R and only them after receiving a gift.
Because Vasya wants to maximise the number of integers he will get, he should buy the smallest and the largest integers available in the shop. They can either appear in the same segment or in different segments. It is important to note that if they appear in the same segment, then it is the longest one.
Let’s add the segments to shop one by one and maintain the following six values:
- The smallest integer in the shop and the cost of the cheapest segment that contains it.
- The largest integer in the shop and the cost of the cheapest segment that contains it.
- The length of the longest segment and the cost of the cheapest of such segments.
It is easy to see that when we add new segment this values can only be updated by parameters of the new segment. When we know all this values it is easy to find how many coins Vasya will spend in the shop.
Since we have set a baseline lets try to code it :
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin>>t;
while(t--)
{
int n;
const int limit = 1e9 + 1;
int min_L=limit, max_R=0;
int min_cost_L=limit, min_cost_R=limit;
int max_length=0, min_cost_length=limit;
cin>>n;
while(n--)
{
int l,r,c;
cin>>l>>r>>c;
if(l<min_L)
{
min_L=l;
min_cost_L=c;
}
if(l==min_L)
min_cost_L=min(min_cost_L,c);
if(r>max_R)
{
max_R=r;
min_cost_R=c;
}
if(r==max_R)
min_cost_R=min(min_cost_R,c);
if(max_length < r-l+1)
{
max_length=r-l+1;
min_cost_length=c;
}
if(max_length==r-l+1)
min_cost_length=min(min_cost_length,c);
int ans=min_cost_L+min_cost_R;
if(max_length == max_R - min_L + 1)
ans=min(ans, min_cost_length);
cout<<ans<<endl;
}
}
return 0;
}
The above solution passes as expected.